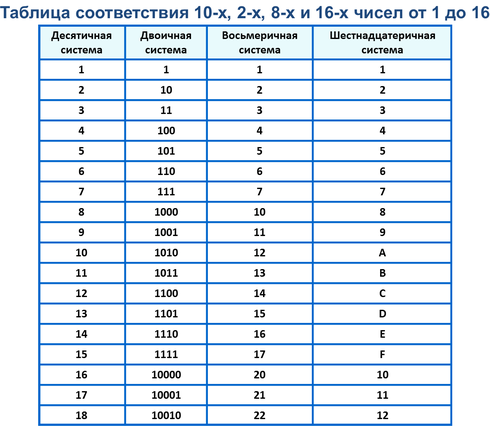
Таблица систем счисления

Двоичное число разбивается на тетрады: целая часть - справа налево; дробная часть - слева - направо; В дробную часть справа можно дописывать недостающее число нулей; Под каждой тетрадой пишется соответствующее шестнадцатеричное число. На этом наш второй урок базового курса по подготовке к ЕГЭ по информатике заканчивается. The Incan Quipu and the Jacobsen Hypothesis англ. Разбор решений некоторых задач 1. Например, дробная часть числа 0, в двоичную систему переводится так удобнее это делать столбиком :.
Мы тут же подберём Вам репетитора. Это бесплатно.

Написать в чат менеджеру. Open menu. Забыл пароль? Из-за блокировщика рекламы некоторые функции на сайте могут работать некорректно!
Пожалуйста, отключите блокировщик рекламы на этом сайте. Для этого нам с вами нужно научится строить таблицу триад и тетрад.
Сделать это очень просто. Таблица заполняется столбиками, поочередно.
Первый столбик - Выписываем 8 нулей, затем 8 единиц. Второй столбик - уменьшаем количество 0 и 1 в два раза, то есть записываем 4 нуля и 4 единицы, повторяем это дважды. Третий столбик - еще в два раза уменьшаем нули и единицы.
Чередуем 2 нуля и 2 единицы до конца столбика. Четвертый столбик - чередуем нули и единицы.

Таким образом мы с вами построили таблицу тетрад нужна для шестнадцатиричной СС , но внутри нее есть есть таблица триад для восьмеричной СС. А внутри таблицы триад, есть таблица диад для четверичной СС.
Для вашего удобства давайте запишем таблицу и выпишем значения для десятичной СС и шестнадцатиричной СС. Давайте представим что у нас с вами есть некоторое шестнадцатиричное число СE5.
Нам нужно перевести это число в двоичную СС. Мы могли бы воспользоваться тем что уже умеем, то есть перевести это число в десятичную СС, а потом в двоичную. Пример одно и тоже число в четырех системах счисления.
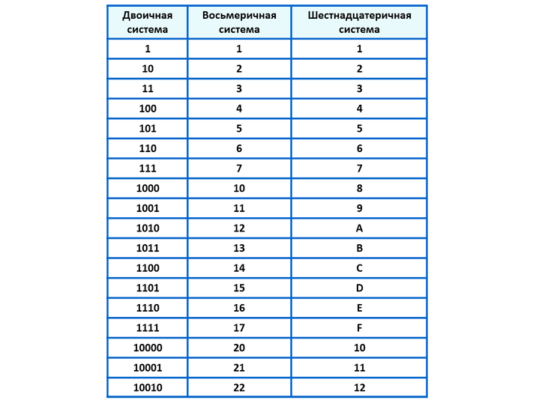
Видно, что наиболее короткую запись имеет шестнадцатеричное число 3 цифры вместо 11 у двоичного. Поэтому в настоящее время помимо двоичной системы счисления в компьютерах используют и шестнадцатиричную.
Кроме того, в некоторых случаях применяется и восьмеричная. Выбор именно этих систем счисления основан на очень простом переводе двоичных чисел в шестнадцатеричные и восьмеричные и обратно.