Принцип гюйгенса френеля кратко

Зонная пластинка — это круглый экран, на котором нанесены кольца так, чтобы перекрывать волны от вторичных источников, которые в результате интерференции гасят друг друга. Фазы вторичных волн отличаются от фаз первичных. Линия L , M , N , перпендикулярная волновому фронту см. Опорные конспекты Г.
Вторая зона. Аналогично определяются границы других зон. Таким образом, если на препятствии укладывается целое число длин волн, то они гасят друг друга и в данной точке наблюдается минимум темное пятно. Если нечетное число полуволн, то наблюдается максимум светлое пятно. Дифракция наблюдается хорошо на расстоянии.

Если , то дифракция невидна и получается резкая тень. Эти соотношения определяют границы применимости геометрической оптики. Если наблюдение ведется на расстоянии ,. На рис.
Можно видеть предметы, размеры которых соизмеримы с длиной световой волны. Дифракционная решетка. Дифракционная решетка - система препятствий параллельных штрихов , сравнимых по размерам с длиной волны.

Оптическая разность хода Из условия максимума интерференции получим:. Следовательно: - формула дифракционной решетки. Jump to Content. Основные ссылки. Почитаем «Физику» вместе Рыбаков А.
Рыбаков Банджи-джампинг, сохранение импульса и уравнение Мещерского Рыбаков А. Волновые фронты сферической волны, которые испускаются при помощи точечного источника, относят к концентрическим сферам.
Далее следует произвести сложение колебаний, учитывая амплитуды и фазы. Элементы, загороженные препятствиями, не учитываются при решении. Для примера ниже приведена дифракционная задача прохождения плоской монохроматической волны, которая исходит от удаленного источника через отверстие с радиусом R непрозрачного экрана.
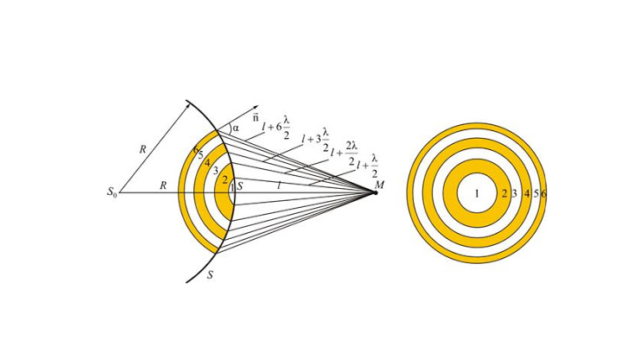
Р — точка наблюдения, находящаяся на оси симметрии, располагаемого на L расстоянии относительно экрана. По принципу Гюйгенса-Френеля распределить на волновой поверхности вторичные источники, совпадающие с плоскостью отверстия, где волны достигают точки Р. Чтобы расчеты были облегченными, волновая поверхность падающей волны разбивается на кольцевые зоны, называемыми зонами Френеля, исходя из правила: расстояния от границ соседних зон к точке Р имеют отличие на половину волны.
При рассмотрении волновой поверхности исходя из точки Р , тогда получим, что границы зон Френеля будут иметь вид концентрических окружностей. Наглядно это изображено на рисунке. По рисунку 3. Значение m может быть любым числом.

От него зависит результат интерференции вторичных волн, проходящих точку Р. Такие открытые зоны Френеля обладают одинаковым значением площади:. По теории равные площади возбуждают колебания с одинаковой амплитудой в точке наблюдения.
Используя приближение, видно, что амплитуда колебаний, которая вызвана определенной зоной, равняется среднему арифметическому соседних зон. Соседние волны начинают гасить друг друга, а это приводит к тому, что суммарная амплитуда в точке запишется как:. Отсюда делаем вывод, что суммарная амплитуда в точке меньше колебаний, вызванных только при помощи одной зоны Френеля.
Если все имеющиеся зоны Френеля являлись открытыми, тогда к точке наблюдения двигалась волна с амплитудой A 0 , невозмущенная препятствием. Тогда запись принимает вид:. Выражения в скобках равняются нулю, значит, амплитуда, вызванная волновым фронтом, равняется половине действий первой зоны.
Когда отверстие непрозрачного экрана дает возможность только одной зоне Френеля быть открытой, тогда наблюдается возрастание амплитуды колебаний в количестве 3 раз, а интенсивности — 4 раз. При открытии двух зон действие становится равным нулю.
При наличии непрозрачного экрана с несколькими нечетными открытыми зонами, очевидно, что произойдет резкое возрастание амплитуды. Полученные пластинки обладают свойством фокусировки света, поэтому их называют зонными пластинками.
Круглый диск дает понять, что при дифракции зоны Френеля от 1 до m будут в закрытом состоянии. Отсюда получаем, что формула амплитуды колебаний примет вид:.
Иначе его называют пятном Пуассона, которое окружается дифракционными кольцами светлого и темного цвета. Ответ: при падении луча перпендикулярно границе раздела.
Чему равен угол отражения? Чему равен угол между падающим и отраженным лучами?
Что произошло с углом между падающим и отраженным лучами? Обсудить ответы на вопросы 7, 8, 9. Обратить внимание на то, что луч падающий, отраженный и перпендикуляр, восставленный в точку падения, лежат в одной плоскости. Повторить закон отражения света. В полном варианте: показать обратимость световых лучей, решить задачи на определение углов падения, отражения и расположения зеркала. Работа на компьютере с рабочими листами.
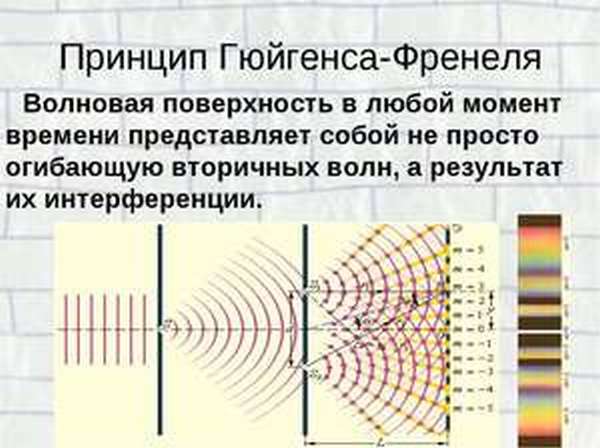
Модель «Отражение и преломление света». Принцип Гюйгенса. Закон отражения света. Цель урока Познакомить учащихся с особенностями распространения света на границе раздела двух сред, дать им сведения о законах, которым подчиняется это явление, дать объяснение этого явления с точки зрения волновой теории света.