Умножение больших чисел в уме

Сначала все может получаться медленно, но потом дело пойдет на лад, и вы сможете быстро считать в уме любые числа. При применении его метода увеличение множителей в два раза потребует проделать всего лишь в три раза больше вычислений. Числа, заканчивающиеся на 5 удобно возводить в квадрат по методу из четвёртого урока. Допустим, у нас получились числа 12 и Стокилограммовую нелетающую птицу назначили верховным хищником эоценовой Антарктиды.
Желание подгонять примеры под определенные математические закономерности часто воспитывается на математических кафедрах в университетах или в школах в классах с математическим уклоном. Людей учат находить простые и удобные алгоритмы решения различных задач. Вот некоторые примеры подгонки:. Сначала считается 49 на сто — Затем делится на 2, что равняется , затем вычитается Итого Из вычитаем , получаем Этот способ может оказаться эффективнее предыдущего только в случае, если вы владеете устным счетом на базе перемножения двузначных чисел на однозначные и можете держать в уме одновременно несколько результатов.
К тому же приходится тратить время на поиск алгоритма решения, а также уходит много внимания за правильным соблюдением этого алгоритма. Способ, когда вы стараетесь умножить 2 числа, раскладывая их на более простые арифметические процедуры, отлично тренирует ваши мозги, но связан с большими мысленными затратами, а риск получить неправильный результат выше, чем при первом методе.
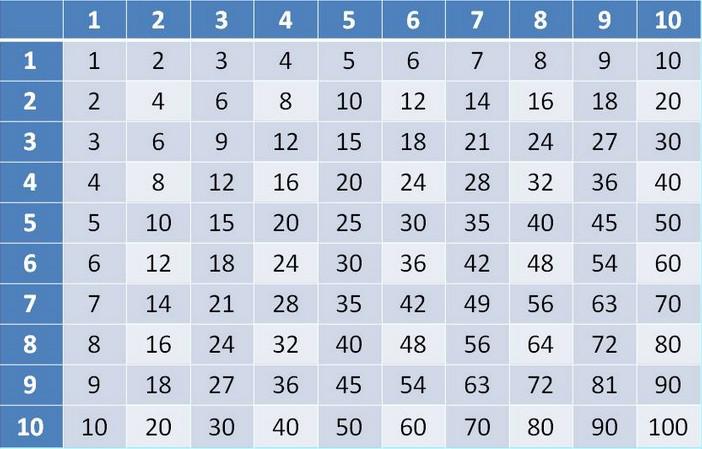
Наверное, счет столбиком содержит максимальное количество действий и требует постоянно держать в уме вспомогательные числа. Но его можно упростить. Во втором уроке рассказывалось, что важно уметь быстро умножать однозначные числа на двузначные. Если вы уже умеете это делать на автомате, то счет в столбик в уме для вас будет не таким уж и трудным. Алгоритм таков. Для этого сведем всю операцию к умножению на однозначные числа. Еще один пример. Умножим 79 на Это значит, что на нужно взять число « 79 » 57 раз.
Разобьем всю операцию на этапы.
Сначала умножим 79 на 50 , а потом — 79 на 7. Вот хитрый прием быстрого устного счета, который поможет умножить любое двузначное число на 11 с феноменальной скоростью. Возьмите любое двузначное число, умножьте его на 11 и убедитесь сами - эта хитрость работает!
С помощью другого интересного приема устного счета можно легко и быстро возводить двузначные числа в квадрат. Особенно просто это делать с числами, которые заканчиваются на 5. Осталось разобраться с делением.
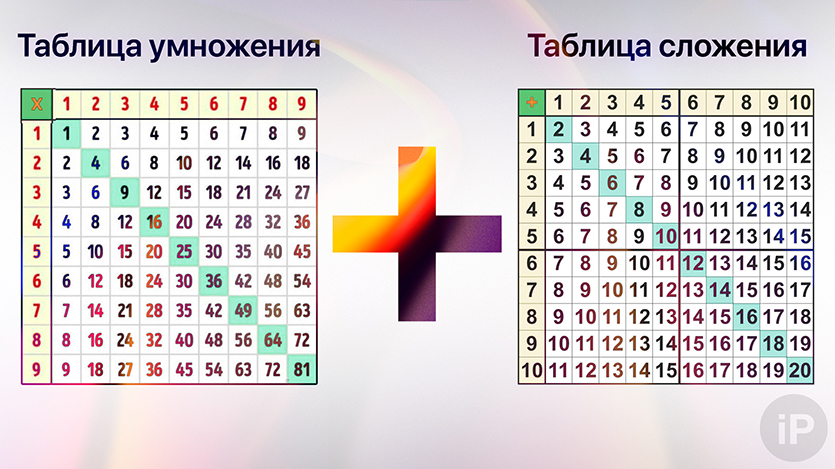
По сути, это операция, обратная умножению. С делением чисел до никаких проблем вообще возникать не должно — ведь есть таблица умножения, которую вы знаете на зубок. При делении многозначных чисел на однозначное необходимо выделить максимально большую часть, которую можно разделить с помощью таблицы умножения.
Например, есть число , которое нужно разделить на 8. Вспоминаем таблицу умножения и понимаем, что на 8 будет делиться число Представим пример в виде:.
Далее из числа также выделяем максимально большое число, которое делится на 8. Осталось разделить 64 на 8 и получить результат, сложив все результаты деления. При делении на двузначное число нужно пользоваться правилом последней цифры результата при умножении двух чисел.
При умножении двух многозначных чисел последняя цифра результата умножения всегда совпадает с последней цифрой результата умножения последних цифр этих чисел. Например, умножим на Первоначально будем пользоваться методом «подгона» и найдем пределы, в которых лежит результат.
Нам нужно найти число, которое при умножении на 56 даст Интуитивно попробуем число Значит, искомое число меньше 80 и явно больше Определим его последнюю цифру. Ее произведение на 6 должно заканчиваться цифрой 4. Согласно таблице умножения, нам подходят результаты 4 и 9.
Логично предположить, что результатом деления может быть либо число 74 , либо Готово, решение найдено! Если бы не подошло число 79 , второй вариант обязательно оказался бы верным.
В заключение приведем несколько полезных советов, которые помогут быстро научиться устному счету:. Польза устного счета неоспорима. Тренируйтесь, и с каждым днем вы будете считать все быстрее и быстрее. А если вам понадобится помощь в решении более сложных и многоуровневых задач, обращайтесь к специалистам студенческого сервиса за быстрой и квалифицированной помощью! Автор: Иван. Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik.
Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Финансовый расчет предприятия. В результате сложения всех результатов и получается искомое 9-значное число. Этот метод называется n2, потому что число n умножается на n несколько раз.
Получите ли вы правильный ответ? Однако еще в году немцы придумали, как ускорить процесс. Напомним, что log — это сокращение от «логарифма», который помогает нам расшифровывать числа, возведенные в степень. Звучит просто, однако по-настоящему логарифмы начинают упрощать процесс в работе с крупными числами. Харви уверен, что метод Шенхаге-Штрассена очень практичен. По его словам, если обычному компьютеру дать задачу перемножить между собой два числа с миллиардом знаков в каждом, используя «школьный» метод — это заняло бы месяцы.
А если дать ему ту же задачу, но использовать при этом подход с логарифмами, то вся операция займет
