Предел шеннона хартли,

Пузаченко, Москва, 9 октября г. С целью минимизации шума квантования он использовал квантователь с большим количеством уровней квантования. Но даже если энергоэффективность процессоров приблизится к пределу Ландауэра, скоро нам просто негде будет хранить информацию. Утверждается, что информация нефизична, неизмерима и нелокальна, что она не подчиняется законам сохранения и может передаваться быстрее скорости света. Конечно, в случае с квантовыми системами это потребует колоссальных вычислительных ресурсов, и гораздо проще было бы моделировать их на квантовом компьютере, который является аналоговой машиной.
Исследовано моделирование уравнения гармонического осциллятора. Проведено сравнение моделирующих сред. Давайте найдем ответ на этот вопрос подробнее.
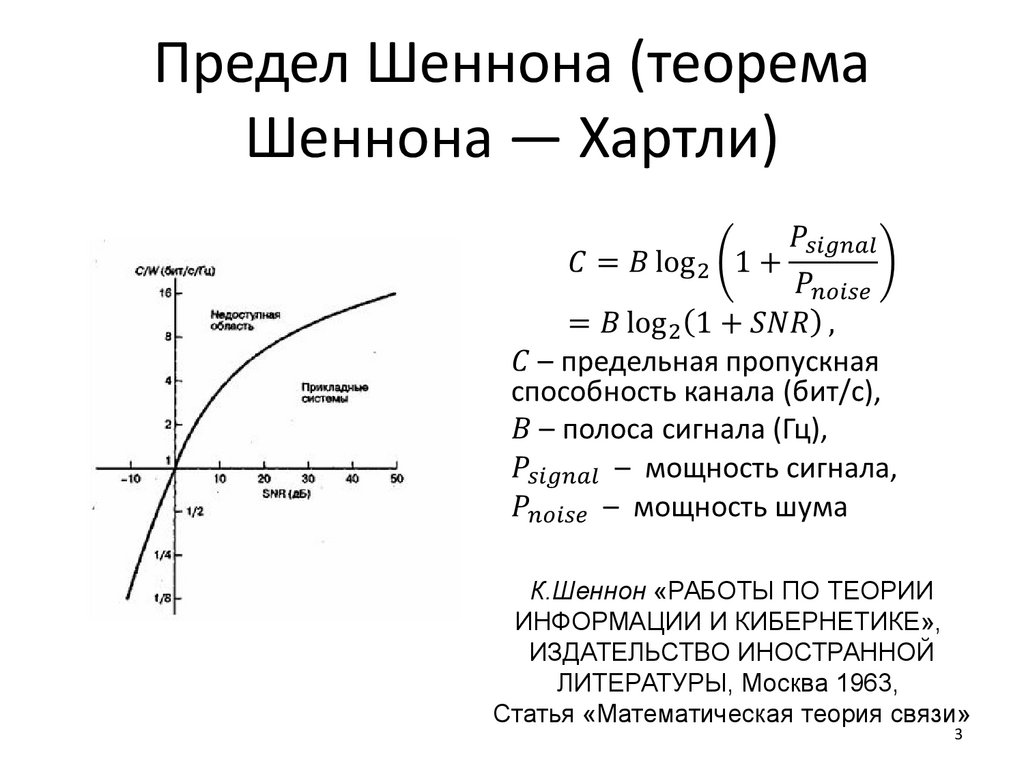
Любая дискуссия о дизайне системы связи будет неполной без упоминания теоремы Шеннона. Теория информации Шеннона сообщает нам количество информации, которую может нести канал. Другими словами, он определяет пропускную способность канала. Теорема может быть сформулирована в простых терминах следующим образом. Данная система связи имеет максимальную скорость передачи информации C, известную как пропускная способность канала. Если скорость передачи информации R меньше, чем C, то передача данных в присутствии шума может происходить со сколь угодно малыми вероятностями ошибок с использованием методов интеллектуального кодирования.
Чтобы получить более низкие вероятности ошибок, кодер должен работать с более длинными блоками данных сигнала. Это влечет за собой более длительные задержки и более высокие вычислительные требования. Теорема Шеннона-Хартли указывает, что при достаточно продвинутых методах кодирования передача, которая приближается к максимальной пропускной способности канала, возможна с произвольно небольшими ошибками. Интуитивно понятно, что для данной системы связи при увеличении скорости передачи информации количество ошибок в секунду также будет увеличиваться.
Уравнение Шеннона-Хартли связывает максимальную пропускную способность скорость передачи в битах , которая может быть достигнута по данному каналу с определенными характеристиками шума и ширины полосы. Для AWGN максимальная вместимость определяется как. Здесь C максимальная пропускная способность канала в битах в секунду, иначе называемая пределом пропускной способности Шеннона для данного канала, B - пропускная способность канала в герцах, S - мощность сигнала в Вт, а N - мощность шума, также в Вт.
Можно убедиться, что максимальная скорость, с которой мы можем передавать информацию без какой-либо ошибки, ограничена шириной полосы, уровнем сигнала и уровнем шума. Он сообщает, сколько битов может быть передано в секунду без ошибок по каналу с шириной полосы частот , когда мощность сигнала ограничена и подвергается воздействию гауссовских белых некоррелированных шумовых аддитивной природы.
Предел пропускной способности Шеннона определен для данного канала. Это фундаментальная максимальная пропускная способность, которая может быть достигнута на канале при любой комбинации любой схемы кодирования, передачи или схемы декодирования. Это лучший предел производительности, который мы надеемся достичь для этого канала. Пропускная способность ограничивает скорость передачи информационных символов по данному каналу. Отношение SNR ограничивает, сколько информации мы можем сжать в каждом передаваемом символе.
Увеличение SNR делает передаваемые символы более устойчивыми к шуму. SNR является функцией качества сигнала, мощности сигнала и характеристик канала.

Измеряется на переднем конце приемника. Таким образом, мы можем обменять пропускную способность на SNR. Однако, поскольку полоса пропускания B стремится к бесконечности, пропускная способность канала не становится бесконечной - поскольку с увеличением полосы пропускания мощность шума также увеличивается.
Стоит упомянуть две важные работы видных ученых до статьи Шеннона [1] , которая заключается в следующем. Предыдущая работа Эдварда Амстронга по частотной модуляции FM является отличным доказательством того, что SNR и полоса пропускания могут быть сопоставлены друг с другом. В году он продемонстрировал, что можно увеличить SNR системы связи, используя FM, за счет выделения большей полосы пропускания [2]. В г. WM Miner в своем патенте патент США , [3] представил концепцию увеличения пропускной способности линий передачи с использованием методов дискретизации и мультиплексирования с временным разделением.
В году А. Ривз в своем французском патенте Патент Франции ,, Патент США 2,, [4] расширил систему, включив в нее квантователь, проложив путь для хорошо известного метода импульсной кодовой модуляции PCM. Он понял, что ему потребуется больше пропускной способности, чем традиционные методы передачи, и использовал дополнительные повторители с подходящими интервалами для борьбы с шумом передачи.
С целью минимизации шума квантования он использовал квантователь с большим количеством уровней квантования. Патент Ривза опирается на два важных факта:. Можно представить аналоговый сигнал например, речь с произвольной точностью, используя достаточную частотную выборку и квантуя каждую выборку в один из достаточно больших предварительно определенных уровней амплитуды. Следовательно, в данном случае в работе Шеннона указано, что теоретически, за счет использования кодирования, производительность можно повысить на 11,2 дБ по сравнению с некодированной двоичной модуляцией.
В настоящее время большую часть такого улучшения почти 10 дБ можно получить с помощью турбокодов см. Оптимальную разработку системы можно наилучшим образом представить как поиск рациональных компромиссов среди различных ограничений и взаимно противоречивых требований.
Компромиссы модуляции и кодирования, то есть выбор конкретных схем модуляции и кодирования для наилучшего использования переданной мощности и ширины полосы, являются очень важными, поскольку имеется много причин для снижения мощности, а также существует необходимость экономии спектра радиочастот.
Для разработки системы связи с определенной способностью к обработке сообщений нужна метрика измерения объема передаваемой информации. Шеннон [3] ввел такую метрику Н , называемую энтропией источника сообщений имеющего л возможных выходных значений. Энтропия entropy определяется как среднее количество информации, приходящееся на один выход источника, и выражается следующим образом. Если сообщение двоичное или источник имеет только два возможных выходных значения с вероятностями р и , выражение для энтропии примет следующий вид.
Если логарифм в уравнении 9. Здесь единица измерения бит — это мера количества информации, и ее не следует путать с термином "бит", означающим "двоичная цифра" binary digit — bit.
Сам термин "энтропия" имеет несколько неопределенный смысл, что вызвано наличием нескольких формулировок в статистической механике. Для информационного источника с двумя равновероятными состояниями например, выбрасывание монеты правильной формы из рис. Как только вероятности уходят от равновероятного состояния, среднее количество информации снижается.
В пределе, когда одна из вероятностей обращается в нуль, H также обращается в нуль. Результат известен до того, как произойдет событие, так что исход не несет в себе дополнительной информации.
Для иллюстрации связи между количеством информации и априорной вероятностью если априорная вероятность сообщения на приемнике является нулем или единицей, сообщение можно не посылать рассмотрим следующий пример.
После девятимесячной беременности женщина оказывается в родильной палате. Муж с волнением ждет в приемной. Через некоторое время к нему подходит врач и говорит: "Примите мои поздравления, вы стали отцом".
Какую информацию отец получил от врача после медицинского исхода! Почти никакой; отец практически достоверно знал, что ребенок должен родиться. Пробелы и знаки пунктуации не учитываются.
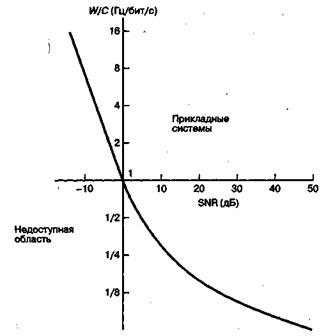
Повторите п. Если 26 букв алфавита нужно выразить в некоторой двоичной схеме кодирования, то для каждой буквы требуется пять двоичных цифр. Пример 9. Подробнее тема кодирования источника будет рассмотрена в главе Пусть по двоичному симметричному каналу определенному в разделе 6.
Одинаково "хороший" прием дает и использование "информации", поступившей из канала, и генерация этой "информации" методом подбрасывания правильной монеты. Утраченной является информация о корректности переданных символов. Для оценки неопределенности в принятом сигнале Шеннон [3] использует поправочный коэффициент, который называет неоднозначностью equivocation. Тогда, используя уравнение 9. Используя формулы 9. Например, кривые вероятности появления битовых ошибок на рис.
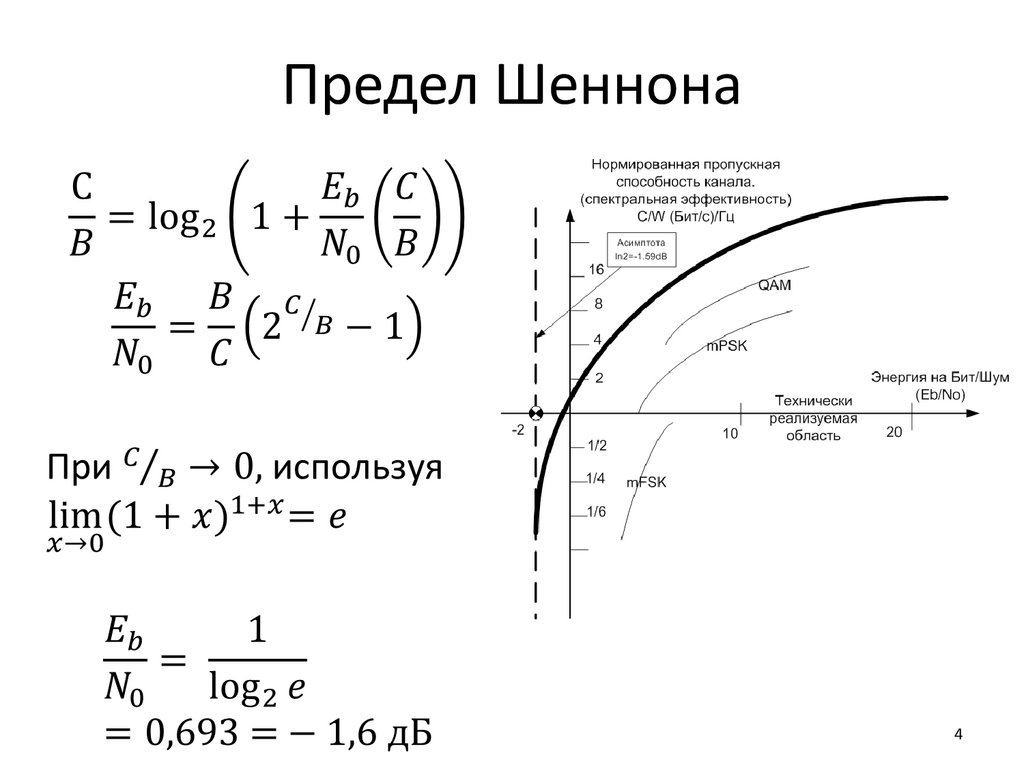
Таким образом, кажется, что всегда при сколь угодно малом значении Eb N 0 имеется ненулевая скорость передачи информации. Предположим, что рабочая точка на рис. Однако Eb , в уравнении 9. Для разрешения описанного выше кажущегося противоречия следует учитывать потери информации, вызываемые помехами канала.
Далее находим неоднозначность и эффективную энтропию.